A Ghost in a Receipt and a Matter of Some Interest

Amasa Southwick was a Quaker born in Bolton, MA in 1778. By 1809 he was living in Leicester, where he was engaged in the manufacture of cards used in processing cotton and wool fibers. The Amasa Southwick manuscript collection¹ at the American Antiquarian Society (AAS) mainly consists of business correspondence and financial documents. An example is the slip of paper shown in Figure 1.

The text of this document is as follows:

                                    Leicester 5^mo 28 1809

                        For value rec^d of Paulina Southic I

                        promis to pay her or order the sum of

                        one hundred and twelve dollars in one

                        yeare frome the above date with interest

                        $112.00                                   Amasa Southic

Southwick’s document is a promissory note. Its format closely follows an example in Michael Walsh’s New System of Mercantile Arithmetic,² shown in Figure 2.

The Southwick note contains a number of interesting features. The date of May 28 is written as 5^mo 28, following the Quaker convention where months and days of the week are written as numbers, avoiding references to non-Christian gods in names such as Saturday or March.³ Paulina and Amasa’s surname is written as Southic, rather than Southwick, perhaps reflecting the pronunciation of the name at that time. Paulina Southwick could be Amasa’s sister Paulina, born in 1788, or an older relative with the same name. After Amasa signed the note in 1809, he would have given it to Paulina. When she received payment Paulina would have returned the note to Amasa, who then crossed out his name. This made the note non-negotiable and showed that the note had been paid. (His signature is visible under the cross-hatched lines of Fig. 1.) The reverse of the Southwick note is shown in Figure 3.

We see that the note was folded to form a narrow oblong, with:

Amasa Southic

Note $112.00

written along the fold. The note would have been kept by Paulina in this folded state for eight years until it was paid in 1817. The date and amount of payment are indicated in two ways.  The right side reads:

                                                 5 mo 28^th 1817

                                                Paid one hundred

                                                seventy eight dollars

                                                fifty cents and ninety

                                                four hundredth,

and on the left we see:

                                                 Paid $178.50.94

                                                5 mo 28^th 1817.

These observations give rise to a number of questions. For example, why was there so much formality in a loan between family members? Today, a person who loans a significant amount of money to a family member would expect repayment, but most people would be unlikely to draft a document with the structure of Southwick’s promissory note.

Compared to other documents from the era, Southwick’s note is typical rather than exceptional. If one was to look at a collection of New England receipts, invoices, and orders from the early nineteenth century, one would see that they are almost universally detailed, precise, and formal, even in the case of modest transactions of one dollar or less. It is a characteristic of that period. We can also address more quantitative questions, as follows.

What was the value of $112.00 in 1809?

We can answer this question in an approximate way by using a tabulation of historical consumer price indices. John McCusker’s 1992 publication⁴ How Much Is That in Real Money? lists consumer price indices which increase from a numerical value of 148 in 1809 to 1,629 in 1991. The ratio of these indices corresponds to an increase in prices by a factor of 11. Using recent data from the Federal Reserve Bank of St. Louis,⁵ there is an additional increase in the consumer price index by a factor of 2.3 from 1991 to 2024. Combining the two increases, one can estimate that consumer prices increased by a factor of 25 from 1809 to 2024. In other words, consumer goods which could be purchased by one dollar in 1809 would cost twenty-five dollars today. Using the factor of 25, we can estimate that the $112 principal of Southwick’s note would have the present-day purchasing power of $2,800.

What was the nature of money in 1809?

Money was complicated in the early nineteenth century. People were familiar with pounds and shillings from the colonial period, and from ongoing trade with Great Britain. American coin denominations, known as Federal money, were relatively new, and there was a shortage of gold and silver coins. To function in an environment where coins were in short supply, foreign coins were accepted in trade. An indication of the importance of Spanish silver coins is shown in Figure 4.

This note says that Southwick is to repay Four hundred and Nine spanish milled Dollars and Fifty eight Cents. The wording implies that the Spanish ocho reales coin, known as the Spanish dollar, was equivalent to the American dollar. The term milled means that the Spanish dollars were machine-made, with a well-defined shape and a decorated edge, in comparison to hammered coins with irregular shapes. As David Martin explains, the Spanish dollar was so important as to appear in the Coinage Act of 1792:

Not until April 1792 did Congress – following essentially the recommendations of Treasury Secretary Alexander Hamilton – authorize an American currency.  The new coinage was based upon a silver dollar “to be of the value of a Spanish milled dollar as the same is now current”…⁶

Well into the nineteenth century, financial quantities in New England transactions were sometimes specified in pounds and shillings. In trade with Great Britain, one would use a conversion rate where one dollar was worth 4 British shillings and 6 pence. But in the local economy things were more complicated. Mathematics books of the period (such as Reference 2) included many sample problems with conversions of colonial currencies. These were denominated in pounds, shillings, and pence, like the British pound and its subdivisions, but the colonial currencies were devalued relative to those of Britain. The complexity of the currencies used at this time is illustrated by Figure 5, from an 1818 mathematics book.⁷

An example of an 1817 financial record involving colonial currency is shown in Figure 6.

This receipt is part of the Gleason & Company papers at AAS.⁸ The item descriptions are difficult to read in this receipt, but the monetary values are clear. They are shown below, with added descriptions.

charge for first item                              1. 10. 0

charge for second item            $6         2.  8.  0

total charge                                           £ 3. 18. 0

credit                                                             12. 0

net charge                                            £  3.   6. 0

payment in dollars                  $8.25/100        Rec’d payment

McFadden’s net charge is 3 pounds and 6 shillings, or 66 shillings, given that there are 20 shillings per pound.  Gleason paid $8.25. There is a conversion at work here which is determined by the ratio:

66 shillings / 8.25 dollars = 8 shillings per dollar.                 [1]

We also get a ratio of 8:1 from the second line, where £ 2.8.0 is written next to $6.00. Since £2.8.0 is  48 shillings, the ratio is 8 shillings per dollar. At first this may seem odd because according to the table in Figure 5, one dollar was worth 4 British shillings and 6 pence. The solution to this puzzle is found by examining the middle portion of the table, where we find that one dollar was worth 8 shillings in New York colonial currency. That is, the pounds and shillings in McFadden’s receipt are not British, they are New York pounds and shillings! We conclude that merchants in Troy, NY were keeping accounts using colonial currency and taking their physical payment in Federal money, that is, dollars. The physical coins were most likely Spanish dollars, given the small numbers of American dollars which had been minted at this time.

The use of colonial New York money in pricing the items in the McFadden receipt may seem quite peculiar to a modern person, because the prices are given in terms of a currency which had no physical existence. In other words, the prices are given in an imaginary currency.  The notion of imaginary money was familiar during this period and the topic was covered in mathematics textbooks, as shown by Figure 7.

Actual payments are made in real money, and imaginary money is used in accounting, therefore economists refer to imaginary money as money of account. During the seventeenth and eighteenth centuries, British colonists in North America used pounds, shillings, and pence in accounting, but there were essentially no British coins available for transactions. Coins were briefly minted in Massachusetts in the latter half of the seventeenth century, but on the whole the coins used in trade were Spanish dollars.⁹ On the basis of silver assays the dollars were equivalent to 4 British shillings and 6 pence, but within the various mainland colonies the dollar was redefined to have higher values, for example one dollar was worth 6 Massachusetts shillings and 8 New York shillings, as shown in Figure 5. According to Curtis Nettles,⁹ “six different rates of colonial money prevailed on the mainland after 1710.” Massachusetts shillings were imaginary, as were New York shillings, and they were not equal to each other!

It might seem that the use of money of account with no relation to the currency in circulation was a peculiar or even unique phenomenon, but the practice was in use for more than one thousand years. Doepke and Schneider point out:

In France, for example, the livre tournois served as a unit of account for centuries during the medieval and early modern periods, even when the corresponding coin was no longer in circulation.  The value of a coin used as an accounting currency could also be different from that of the same coin in circulation, a phenomenon referred to as “ghost money”…¹⁰

Thus we see that in the early nineteenth century, financial transactions were complicated by a shortage of coins, the American dollar was based on a Spanish coin, and accounting was sometimes in terms of ghostly pounds and shillings used as monies of account.

Returning to Amasa Southwick’s promissory note in favor of Paulina Southwick (Figures 1 and 3), we address the initial loan amount and the remarkable value, specified in hundredths of one cent, which was paid after eight years. From the front of the note (Figure 1) we see that the original loan was $112.00 on May 28, 1809.  From the back (Figure 3) the repayment was $178.5094 on May 28, 1817. How was this value calculated? Why was repayment specified to one one-hundredth of one cent? Is the number accurate? What was the interest rate?

We begin by noting that the interest allowed by Massachusetts usury laws was 6%, so we will try this rate. For a one-year loan, the interest would be:

6% ($112.00) = 0.06 × $112.00 =   $6.72                           [2]

If the eight-year loan involved simple interest, the same interest would accrue every year, leading to $53.76 over eight years. The balance due at the end of the loan period would be the principal ($112.00) plus the interest ($53.76), that is, $165.76. This value is less than what Southwick paid, so next we suppose that he paid compound interest. In this case the interest paid in a given period is based on the balance during that period, with increasing values of the balance over the course of the loan. Consider the case of annual compounding with an interest rate of 6%.  If the initial value of the loan is P, the interest in the first year is 0.06 P. The balance B₁ at the end of the first year is:

B₁ = P + 0.06 P = (1 + 0.06) P = 1.06 P.                            [3]

That is, the loan balance increases by a factor of 1.06 during the first year. The rate of increase is the same during all succeeding years, therefore at the end of two years the balance is:

B₂ = 1.06 (1.06 P) = (1.06)² P.                                     [4]

Continuing this process, at the end of eight years the loan balance is:

B₈ = (1.06)⁸ P.                                                   [5]

According to Equation 5, the amount which is due after eight years of an annually compounded 6% loan is the initial value of the loan multiplied by (1.06)⁸.

The quantity (1.06)⁸ is what Amasa Southwick (or Paulina) would need to use in order to determine the amount due after eight years. There are at least three ways to determine this number, as follows.

1. We could determine (1.06)⁸ by multiplying directly, that is:
   (1.06)⁸ = 1.06 × 1.06 × 1.06 × 1.06 × 1.06 × 1.06 × 1.06 × 1.06This calculation is tedious but can be done by a patient person. Using a hand calculator, we get (1.06)⁸ = 1.59384808. Substituting into Equation 5 we get the balance due:

                          B₈ = 1.59384808 × 112.00 = 178.51098                         [6]

   Rounding to hundredths of a cent (as in Amasa’s note), the amount due is $178.5110. This value is 16 hundredths of one cent larger than Amasa’s value on the back of his note.

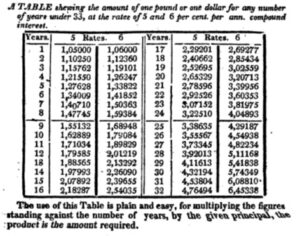
2. Promissory notes and corresponding interest calculations were common in the nineteenth century; therefore, interest tables were published in numerous math textbooks and handbooks. As an example, Figure 8 is from p. 119 of Reference 2.

   

   Using the value given in this table for an eight-year loan at 6%, Amasa’s balance due would be 1.59384 × 112.00 = 178.51008.  Rounding to hundredths of one cent we get $178.5101. This value is 7 hundredths of one cent higher than Amasa’s value and 9 hundredths lower than the exact value given in section 1.

3. The third method employs logarithms, using techniques which were widely studied in the early nineteenth century, for example using Burritt’s text.⁷ The speed and flexibility of this method is based on a property of the logarithm for a number raised to a power. For example, in our case we would use:

   log (1.06)⁸ = 8 log (1.06)                                        [7]

   Using logarithm values from the table in Reference 7 we get:

   log (1.06)⁸ = 8 × 0.0253059 = 0.2024472                         [8]

   Then we use the logarithm table a second time to get:

   (1.06)⁸ = 1.5938                                             [9]

   and the balance due would be 1.5938 × $112.00 = $178.5056. This value is 38 hundredths of one cent lower than Amasa’s value, and 54 hundredths lower than the exact value. Some of the details in using the logarithm method have not been explained here, in the interest of brevity.

Our modern world is sophisticated and complicated in many ways, but when it comes to financial transactions many of us employ a sort of “point and click” approach, perhaps not even bothering to maintain a detailed record of our transactions. When we look at the small bits of paper which are our record of nineteenth century invoices, receipts, and loans, they may not seem very interesting at first glance. But there are interesting data in those bits of paper, involving the people taking part in a transaction, the things which people were buying, labor rates, and as we have addressed here, the mathematical methods used in the calculation of loan balances.

Frank Lamelas did a Ph.D. in physics at the University of Michigan and then he was a postdoc at AT&T Bell Labs and the University of Missouri. He taught physics at Marquette University, Boise State University, and Worcester State University. His experimental research involved x-ray and neutron scattering, surface science, crystal growth, high-pressure cells, and optics. Currently he reads manuscripts as a volunteer at AAS.

References

1. Amasa Southwick papers, American Antiquarian Society 364115.
2. Michael Walsh, A New System of Mercantile Arithmetic; Adapted to the Commerce of the United States, in its Domestic and Foreign Relations; with Forms of Accounts and Other Writings Usually Occurring in Trade, 4th ed. (E. Little & Co., Newburyport, 1814), American Antiquarian Society 312042.
3. Samuel G. Barton, The Quaker Calendar, Proc. American Phil. Soc. 93, 32 (1949).
4. John J. McCusker, How Much Is That in Real Money? A Historical Price Index for Use as a Deflator of Money Values in the Economy of the United States (American Antiquarian Society, Worcester, 1992).
5. Economic data are posted by the Federal Reserve Bank of St. Louis at fred.stlouisfed.org.
6. David A. Martin, The Changing Role of Foreign Money in the United States 1782-1857, J. Econ. Hist. 37, 1009 (1977).
7. Elijah Hinsdale Burritt, Logarithmick Arithmetick Containing a New and Correct Table of Logarithms of the Natural Numbers from 1 to 10,000, Extended to Seven Places Besides the Index; and So Contrived, That the Logarithm May Be Easily Found to Any Number Between 1 and 10,000,000 (Ephraim Whitman, Williamsburgh, 1818), American Antiquarian Society 293540.
8. Gleason & Company papers, American Antiquarian Society 530276.
9. Curtis Nettles, British Policy and Colonial Money Supply, Econ. Hist. Rev. 3, 219 (1931).
10. Matthias Doepke and Martin Schneider, Money As a Unit of Account, Econometrica 85, 1537 (2017).